吴恩达机器学习课程_个人笔记

课程来源：https://www.bilibili.com/video/av9912938

2 单变量线性回归 Linear Regression with one variable 本文链接

2-1 模型表示Model Representation

以上述预测房价为例 线性回归 \(H_\Theta {(x)}=\theta_0+ \theta_1 {(x)}\)

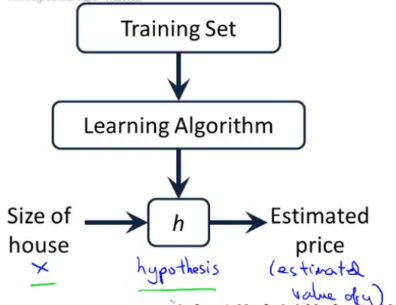
2-2 代价函数Cost Function

代价函数也称误差函数

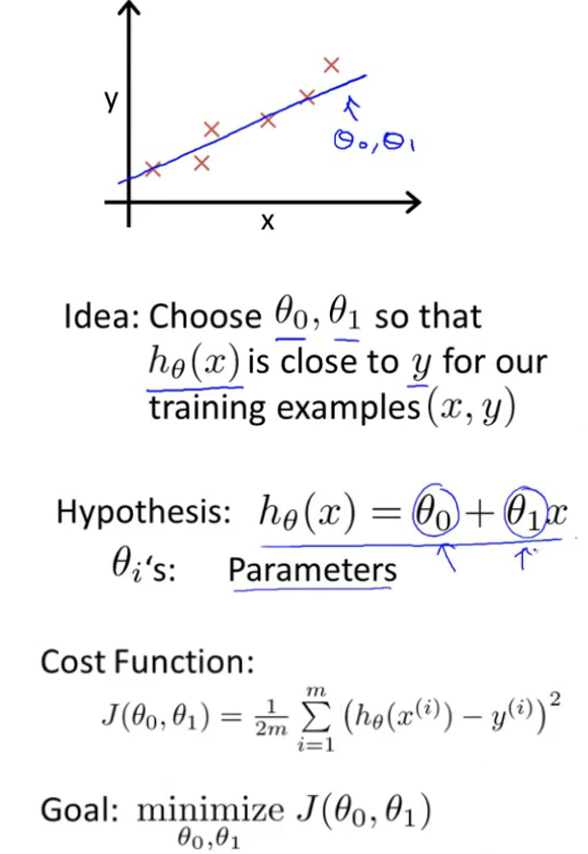
2-3 代价函数举例1 Cost Function - Intuition I

举例说明代价函数的计算方法：简单的，当\theta_0 =0\)时；代价函数只有一个参数。

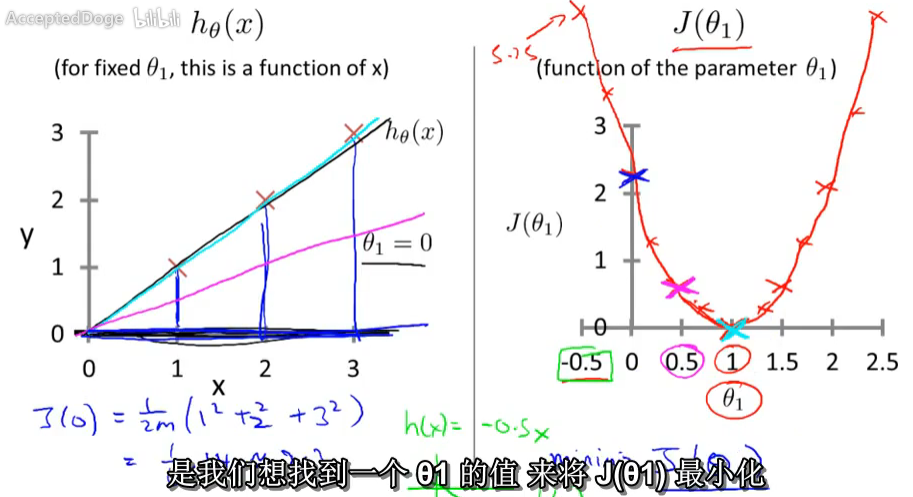
2-4 代价函数举例2 Cost Function - Intuition II

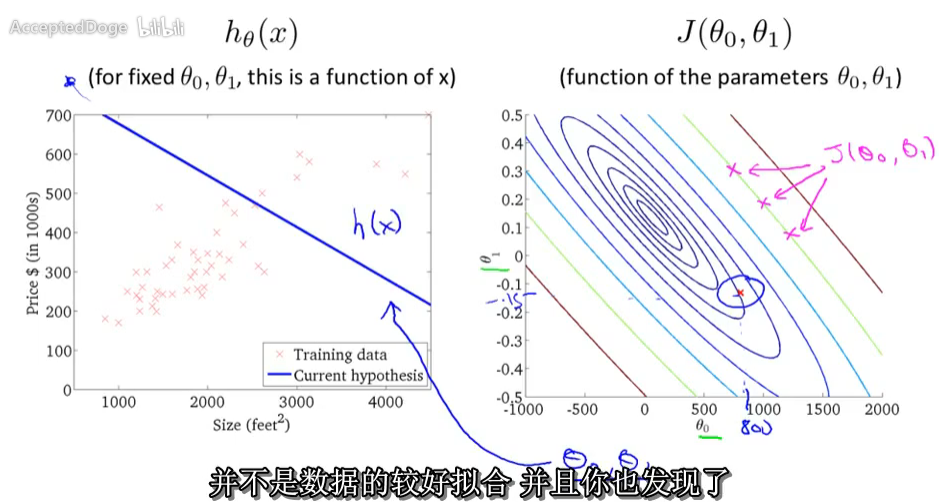
举例说明代价函数。代价函数有两个参数。曲面图。 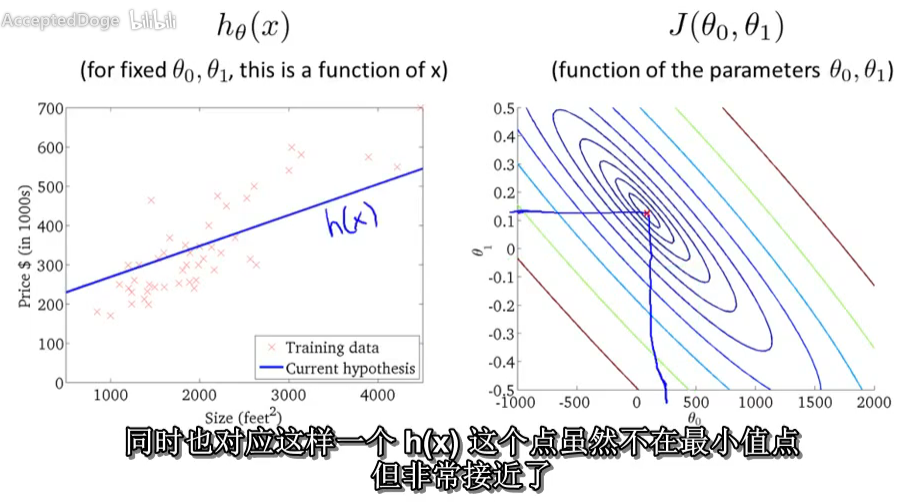我们需要一个算法，来寻找使得代价函数最小的参数θ0和θ1。

2–5 梯度下降算法 Gradient Descent

Learning Rate 相当于步长，下山每一步的长度。 同时更新Simultaneous update所有参数（此处是0和1）。

2-6 梯度下降算法举例 Gradient Descent Intuition

1举例说明 当只有一个参数 2当学习率（步长）取得太小，下降速率就太慢；学习率太大，下降速率太快，有可能跳出最优解，也有可能发散。 当接近局部最优解时，梯度（导数）越来越小，梯度下降的步长（减去项）越来越小，因此没有必要手动减小学习率。

2–7 线性回归中的梯度下降 Gradient Descent For Linear Regression

将梯度下降算法应用到线性回归中，并举例说明。