吴恩达机器学习课程_个人笔记

课程来源：https://www.bilibili.com/video/av9912938

4 多变量线性回归 Linear Regression with multiple variable

这一章主要是把第2章的单变量变成多变量来讲述，更加具有一般性。

4-1 多个特征量Multiple Features

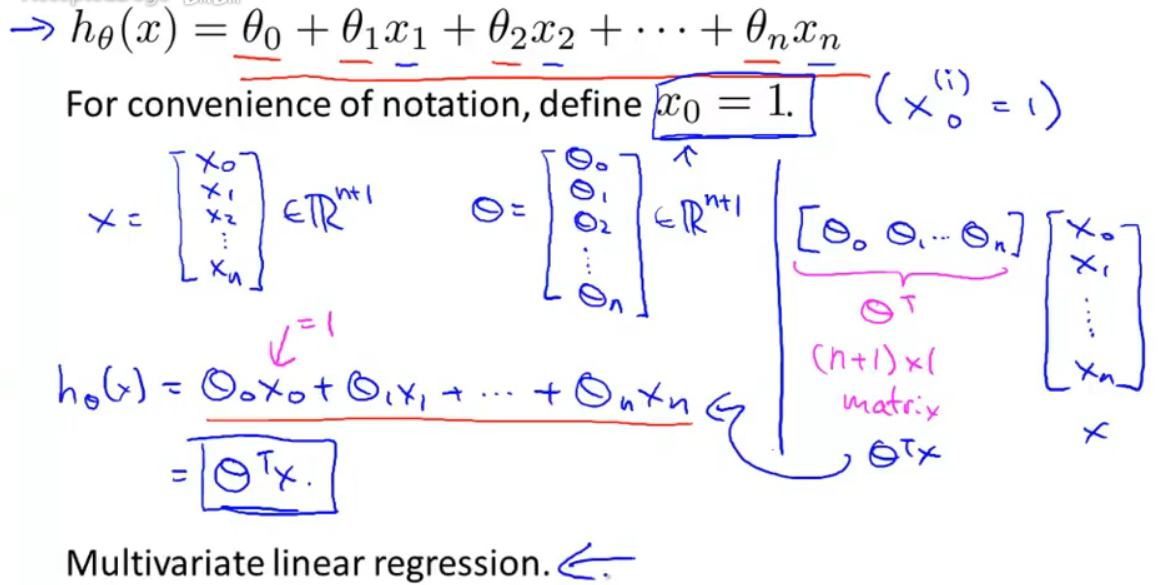
如果使用多个特征量输入x=[x0，x1，…,xn] ,自然也有多个参数需要训练。 这就叫做多元线性回归（Multivariate Linear Regression）

4-2 多个特征量的梯度下降Gradient Descent for Multiple Variables

特征量有多个，hx的自变量有对个，可学习参数也有多个。

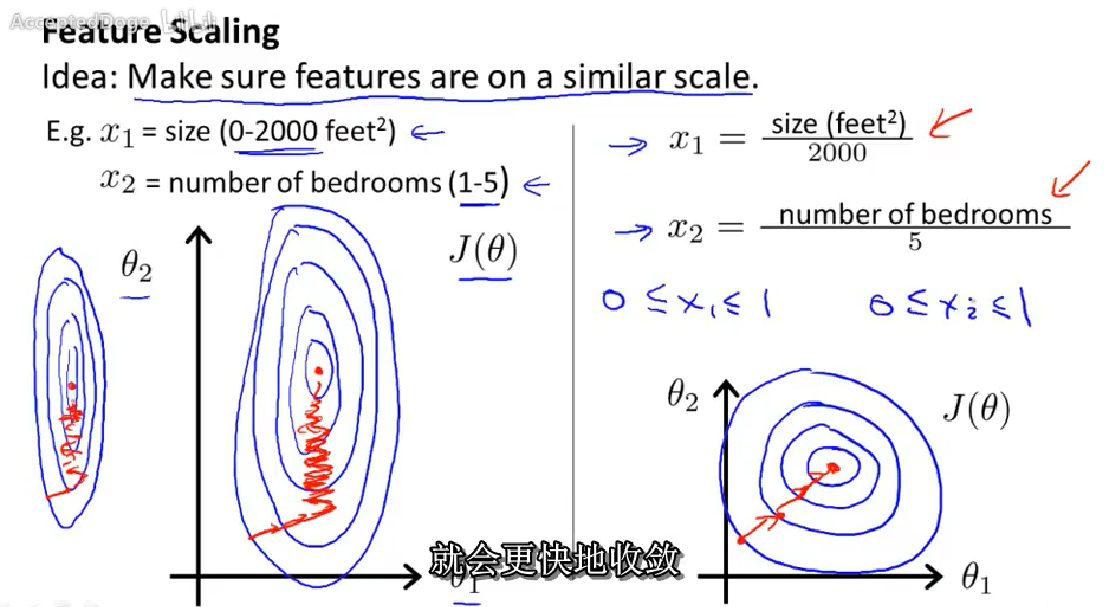
4-3 梯度下降-特征缩放Gradient Descent in Practice I - Feature Scaling

特征量缩放（归一化），能更快地收敛。

4–4 梯度下降—学习率Gradient Descent in Practice II - Learning Rate

1调试：如何使得梯度下降正确工作。 在迭代进行时，计算每次迭代之后的误差值。画出误差值-迭代次数曲线。 a.每次迭代之后，误差值应当减小。如果误差值不再减少，说明基本上已经收敛了。 b.如果使用误差函数的值是否小于某一个阈值，来判断迭代是否收敛 如果误差值一直增大，说明学习率可能太大了。 2 如何选择学习率α 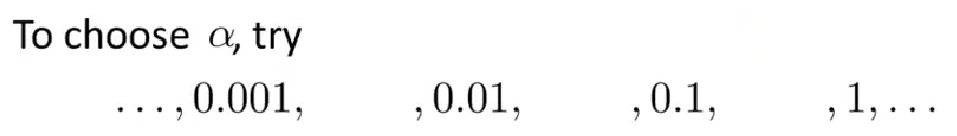作者一般按照3的倍数来取值

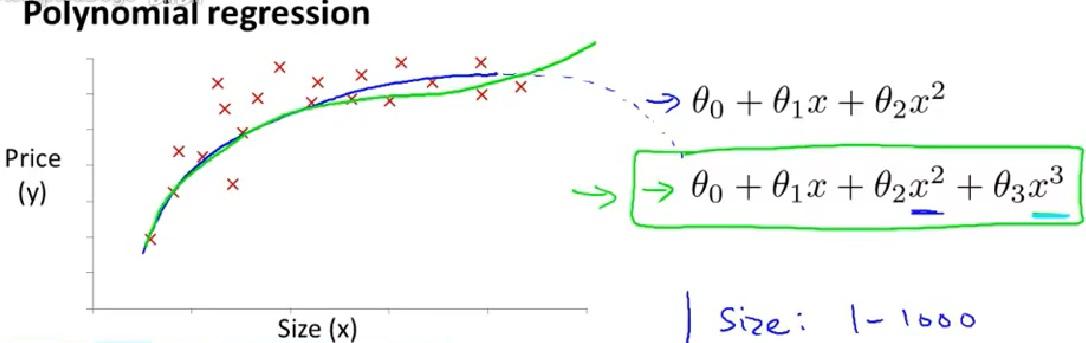
4-5 特征与多项式回归Features and Polynomial Regress

选择特征的方法。选择多样性。 多项式回归。（二次函数,三次函数…）举例说明此样本三次函数好一些一些

4-6 标准方程法Normal Equation

求解误差函数的最小值的方法

• 梯度下降法：多次迭代得到最优解。
• 标准方程法：使用解析解。

标准方程法，令误差函数的导数为零，解得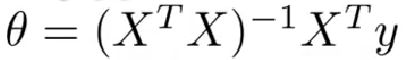： 最小二乘法https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=aladdin

4-7 标准方程法的不可逆性 Normal Equation Noninvertibility (Optional)

使用标准方程法求解误差函数的最小值时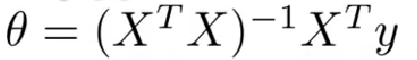，有时无法求逆。

1. 多余特征，x之间线性相关，x‘*x无法求逆。解决：删除多余特征。
2. 太多的特征，也会不好操作。解决：删除一些特征；使用正则化方法。后续讲解。