机器学习笔记_6_逻辑回归

吴恩达机器学习课程_个人笔记

课程来源：https://www.bilibili.com/video/av9912938

#6 逻辑回归 Logistic Regression

这章主要是讲解逻辑回归，主要就是把原来线性回归的假设函数后面添加了一个激活函数。 由于第5章主要讲解Octave的使用方法，与Matlab相似我就不再赘述了。

6-1 Classification

使用线性回归解决分类问题，不太合适，需要改进。 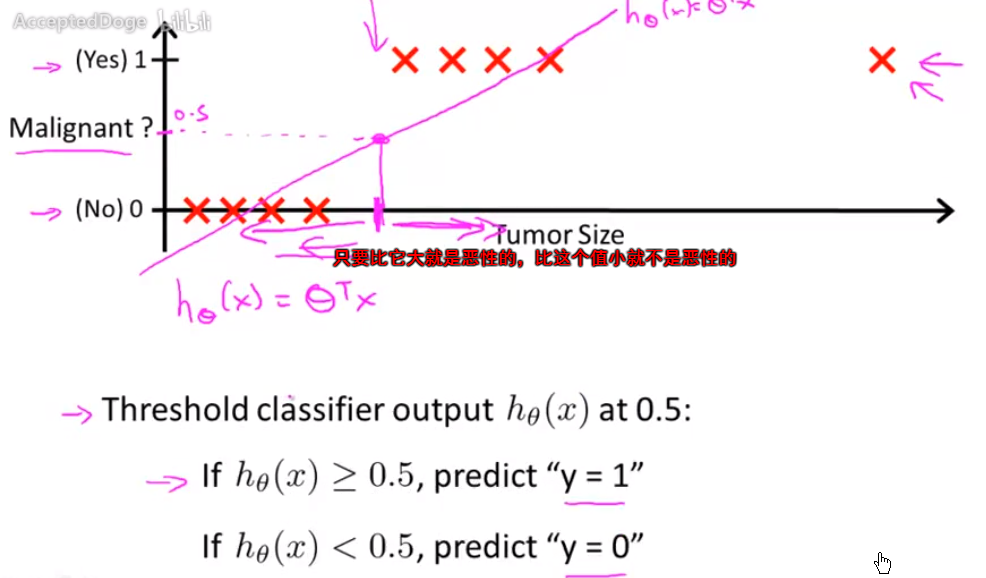问题：为什么不能做一个x=b这样的分类函数。

6-2 假设函数Hypothesis Representation

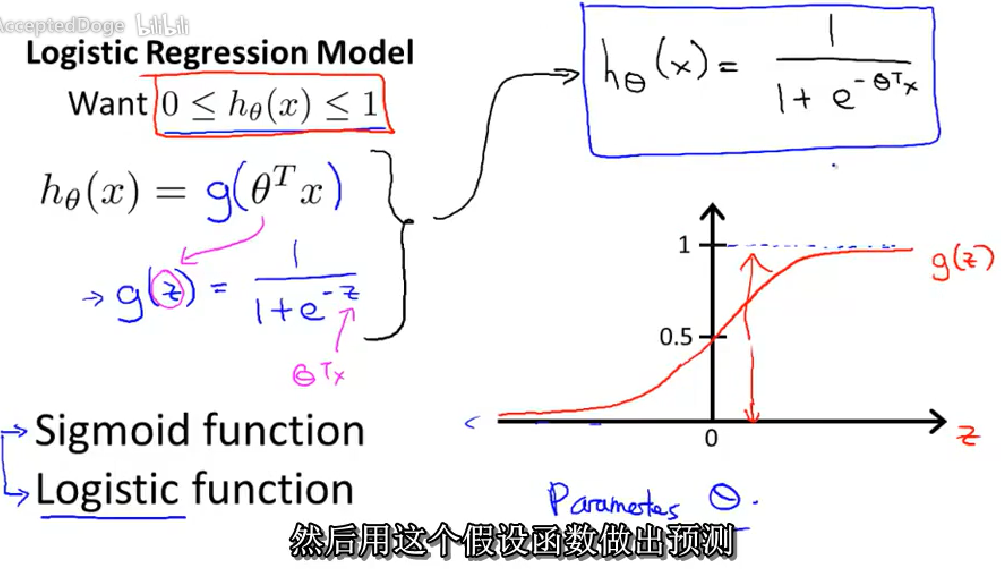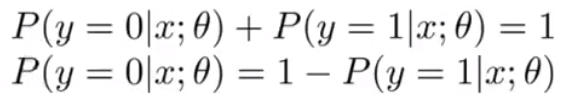在分类问题中，要用什么样的函数来表示我们的假设。 1、在原来的h（x）之后添加一个激活函数得到新的h（x）。使得输出在(0,1)范围内。 2、对h（x）的理解，对于输入x，y=1的概率。 所以： 所以我觉得线性回归于逻辑回归的区别就是，逻辑回归增加了激活函数，以适应分类问题。

6-3 决策边界Dicison Boundary

1 激活函数为sigmiod时，如上图。 假设当假设函数h大于0.5时，预测结果y=1；当假设函数h小于0.5时，预测结果y=0。 那么相当于，当 大于零时，预测结果y=1；当 小于零时，预测结果y=0； 2 举例说明上述问题，并解释决策边界 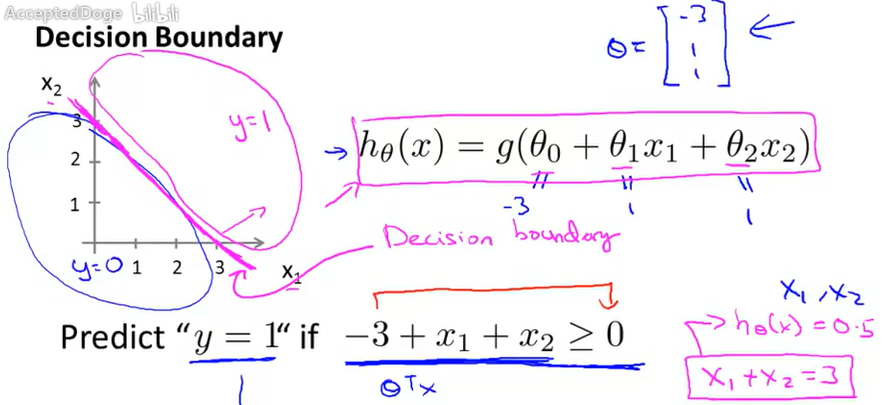图中紫色直线是本例假设函数的决策边界。 决策边界是决策测试数据的属性（分类结果）的边界。 决策边界是假设函数以及参数的属性，不是数据集的属性。 训练数据集用来拟合参数。只要给定参数向量。决策边界便可以完全确定。 3 非线性决策边界 增加更加复杂的多项式，可以得到更加复杂的决策边界。

6-4 代价函数 Cost Function

如何拟合逻辑回归模型的参数。 1 给定训练集和假设函数h（x），我们如何来拟合参数θ？（代价函数） 2 在逻辑回归中，如果直接使用线性回归中的代价函数——平方函数，那么他会变成参数θ的非凸函数。为什么？因为有了激活函数的使用，使得代价函数（平方函数）有许多局部最优值。 3 逻辑回归中的代价函数 线性回归的代价函数 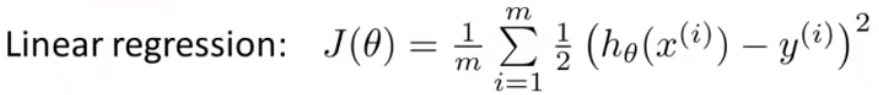逻辑回归的代价函数（对于二分类问题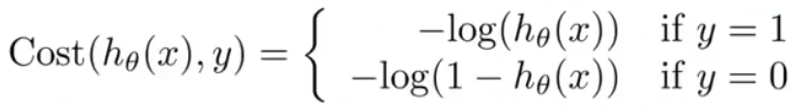） 当y=1时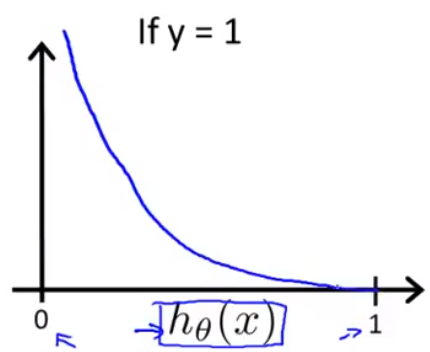， 如果h（x）=1，那么cost=0； 但是当h（x）—>0时，cost —>∞。预测值h（y=1|x）=0，但是真实值y=1。我们使用了一个非常大的代价值来惩罚这个学习算法。 当y=0时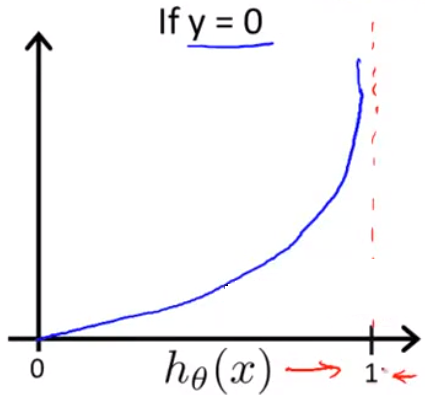， 同理，当预测错误时，也使用一个很大的代价值来惩罚学习算法。

6-5简化代价函数和梯度下降 Simplified Cost Function and Gradient Descent

简单的方法来写代价函数，替换上一节中的代价函数。如何使用梯度下降算法来拟合参数。 1 把上一节中y=1和y=0的情况合起来写成一个式子。 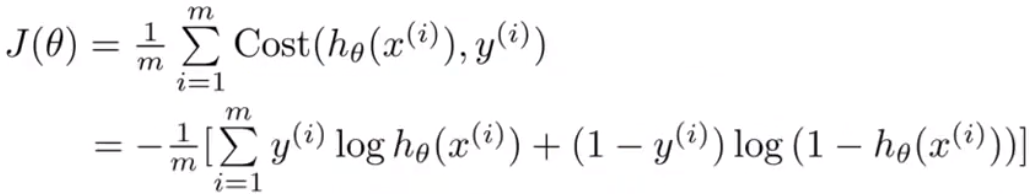2 使用梯度下降来使得代价函数最小 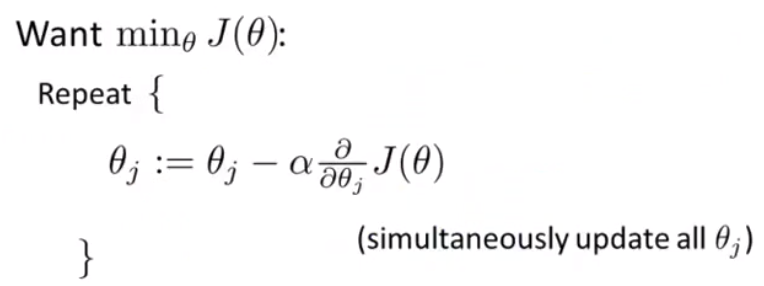代入可得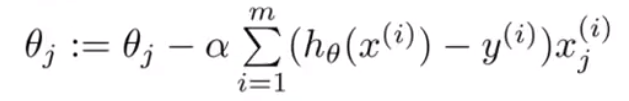： 我们发现，这里于之前线性回归的梯度下降的更新规则形式上相同。但是假设函数不一样，所以继续代入就会不一样。

6-6 高级优化算法 Advanced Optimization

高级优化方法，来提高逻辑回归梯度下降的速度。 1 给定一个代价函数，使用梯度下降使得其最小。编写代价函数的代码和代价函数的导数的代码，然后将其带入到梯度下降算法中迭代，求最小。 2 使得代价函数最小的优化算法并不止梯度下降算法一种，还有其它的一些优化算法，比如：共轭梯度法，BFGS（变尺度法），L-BFGS（限制变尺度法）。（工程优化-最优化计算方法） 这三种算法的优点是：不需要手动选择学习率，一般比梯度下降快。缺点是：比较复杂。 3 举例说明 略

6-7 多分类问题 Multiclass Classification_ One-vs-all

如何使用逻辑回归来解决多分类问题，one-vs-all 算法 1 多分类问题。邮寄分类；疾病判断，天气预测。 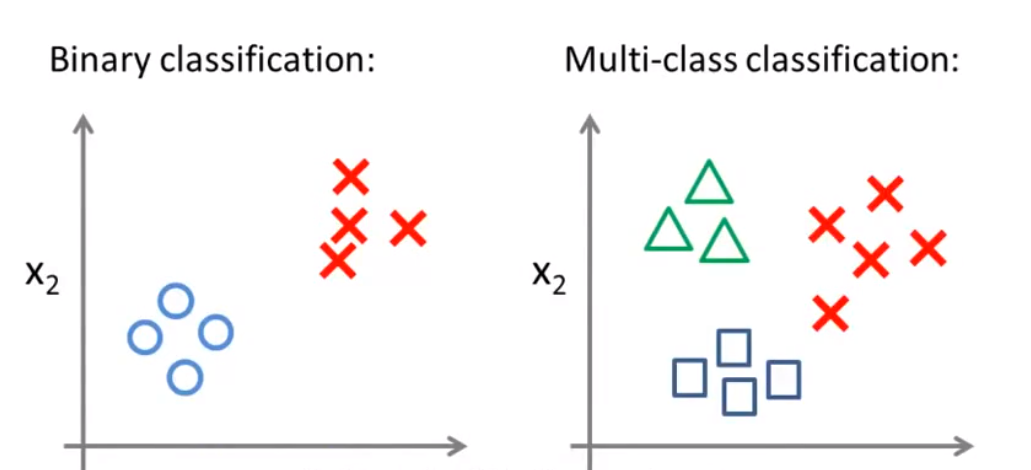2 one-vs-all 算法 一对多算法 原理：将多分类问题转换为多个二分类问题。 举例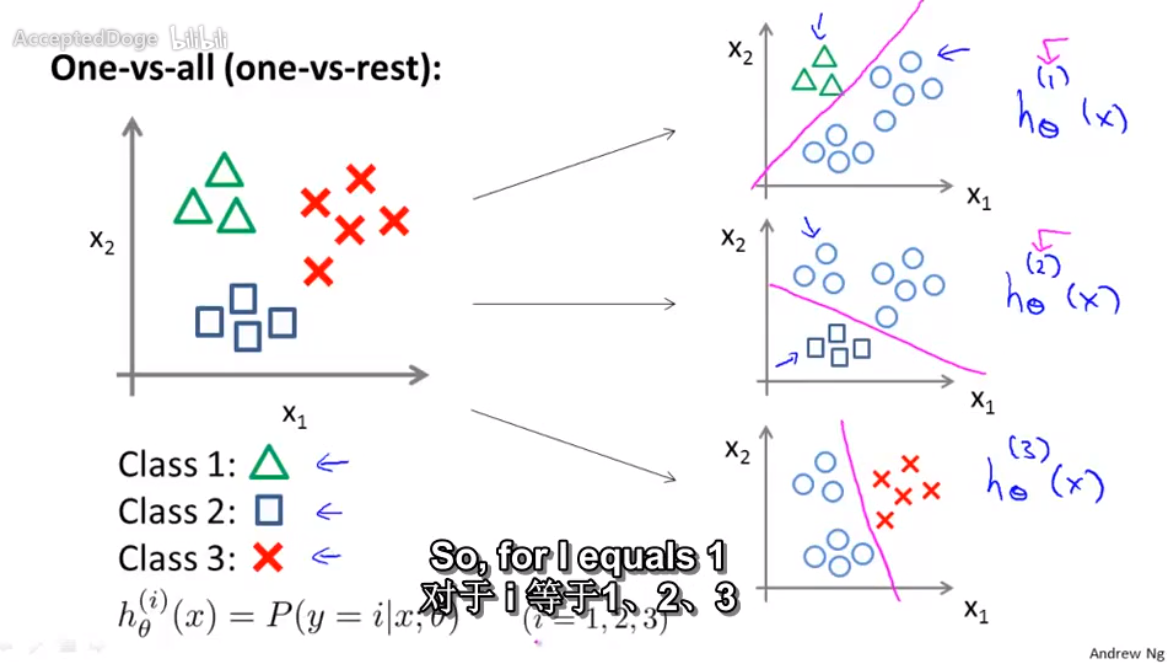： 在同一个数据集上使用逻辑回归来训练三个二分类分类器，得到三个训练好的分类器。 测试时，选择假设函数最大的分类结果。